Teorema de Laplace

La teorema de Laplace es un algoritmo para encontrar el determinante de una matriz. La teorema de Laplace también es llamada extensión por los menores de edad y extensión por los cofactores. La teorema de Laplace se nombra después del matemático francés Peter Simon Laplace (1749-1827).

Para encontrar un determinante de una matriz por la teorema de Laplace:

• Seleccione cualquier fila o columna de la matriz;
• Encuentre al menor de edad de cada elemento en la fila o la columna seleccionada;
• Agregue o reste cada elemento multiplicado por el su cofactor.

La fórmula para la teorema de Laplace de una matriz A del n×n es: donde está el a_ij un elemento de la matriz y del c_ij es el cofactor del a_ij del elemento.

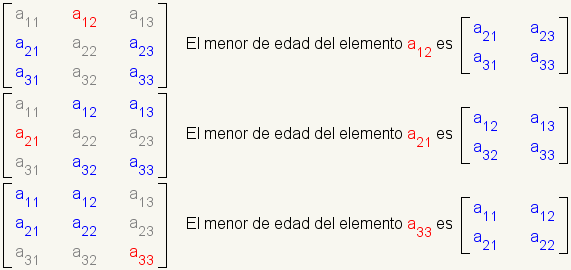
El menor de edad de un elemento de una matriz es la matriz cuadrada formada fuera de la matriz excluyendo la fila y la columna del elemento. Véase el cuadro 1. El cofactor de un elemento de una matriz es el determinante del menor de edad de ese elemento.

Cuadro 1: Menores de edad de una matriz 3×3.

Cuadro 2: Muestras de los cofactores para una matriz 2×2. Cuadro 3: Muestras de los cofactores para una matriz 3×3.

Cuadro 4: Muestras de los cofactores para una matriz 4×4. A si un elemento y su cofactor están añadiros o restados del resultado depende de la posición del elemento en la matriz. Figura que 2, 3, y 4 demuestran si un elemento particular está agregado o restado. Para construir la ecuación para la teorema de Laplace, multiplique cada elemento de la fila seleccionada o la columna por su cofactor y aplique la muestra. Asuma, por ejemplo, la columna 3 se selecciona. La ecuación entonces está:

Ejemplo

Paso	Figura	Descripción
1		Encuentre el determinante 3x3 de la matriz A por la extensión del cofactor.
2		Seleccione una fila o una columna para ampliarse. Puesto que el elemento a22 es cero, hace cálculos más fáciles. Se selecciona la fila 2.
3		Comience con el elemento a21. Encuentre el cofactor de a21.
4		Calcule el valor del cofactor de a21.
5		Puesto que a22 es cero, no es necesario calcular el valor del cofactor de a22 desde 0·x = 0.
6		Ahora encuentre el cofactor del elemento a23.
7		Calcule el valor del cofactor de a23.
8		Utilice la ecuación del cofactor para encontrar el determinante.
Cuadro 1: Extensión de Laplace.

Más información

• cofactor. buscon.rae.es. Real Academia Española. 2009-04-03. http://buscon.rae.es/draeI/SrvltConsulta?TIPO_BUS=3&LEMA=cofactor.

Citar este artículo como:

Teorema de Laplace. 2009-04-03. Enciclopedia de Todas las Palabras de la Matemáticas. Life is a Story Problem.org. https://www.allmathwords.org/es/l/laplaceexpansion.html.

Traducciones

• Click here to see this article in English.

créditos de imagen

• Todas las imágenes y manipulatives están por David McAdams a menos que estén indicadas de otra manera. Todas las imágenes de David McAdams son & de los derechos reservados; © Life is a Story Problem.org y se puede reproducir para el uso educativo no comercial solamente.

La historia de revisión

2009-04-03: Traducido automáticamente por BabelFish. (babelfish.yahoo.com.)
2009-01-08: Versión inicial (McAdams, David.)